It’s time for the 227th meeting of the American Astronomical Society! A number of BDNYC members are there to present talks and posters so be sure to check them out! In this post we list the times and dates various posters/talks so you can go check them. We’ll be posting links to the posters as well once the conference is over.
BDNYC (and friends) are out in force for the 225th meeting of the American Astronomical Society!
Please come see our posters and talks (mostly on Monday). To whet your appetite, or if you missed them, here are some samplers:
Munazza Alam (Monday, 138.40)
High-Resolution Spectral Analysis of Red & Blue L Dwarfs
Sara Camnasio (Monday, 138.39)
Multi-resolution Analysis of Red and Blue L Dwarfs
Kelle Cruz and Stephanie Douglas (Monday, 138.37)
When good fits go wrong: Untangling Physical Parameters of Warm Brown Dwarfs
Stephanie Douglas (Monday 138.19)
Rotation and Activity in Praesepe and the Hyades
Jackie Faherty (Talk, Monday 130.05)
Clouds in the Coldest Brown Dwarfs
Joe Filippazzo (Monday, 138.34)
Fundamental Parameters for an Age Calibrated Sequence of the Lowest Mass Stars to the Highest Mass Planets
Paige Giorla (Monday, 138.44)
T Dwarf Model Fits for Spectral Standards at Low Spectral Resolution
Kay Hiranaka (Talk, Monday 130.04D)
Constraining the Properties of the Dust Haze in the Atmospheres of Young Brown Dwarfs
Erini Lambrides (Thursday, 432.02)
Can 3000 IR spectra unveil the connection between AGN and the interstellar medium of their host galaxies?
Emily Rice (Tuesday, 243.02)
STARtorialist: Astronomy Outreach via Fashion, Sci-Fi, & Pop Culture
Adric Riedel (Monday, 138.38)
The Young and the Red: What we can learn from Young Brown Dwarfs
In my first serious foray into Python and github I adapted some plotting code from Dan Foreman_Mackey with the help of Adrian Price-Whelan and Joe Filippazzo to create contour plots and histograms of my fitting results! These are histograms MCMC results for model fits to a low-resolution near-infrared spectrum of a young L5 brown dwarf, in temperature and gravity atmospheric parameters. The colors represent different segments of the spectrum – purple is YJH, blue is YJ, red is H. The take-away is that different segments of the spectrum results in different temperatures, and all parts of the spectrum make it look old (high gravity). This is probably because the overly-simplistic dust treatments in the models are not sufficient for young, low-mass objects.
The baseline for comparison is the result for a field L5 dwarf, shown below. The temperatures are much more consistent with one another and what you would expect for an L5 spectral type from other methods, and the gravities are similarly high (although too high for comfort for J band). This is reassuring for the method in general and probably means that we need most sophisticated dust treatments in the models to handle giant-exoplanet-like young brown dwarfs. Paper will be submitted soon!
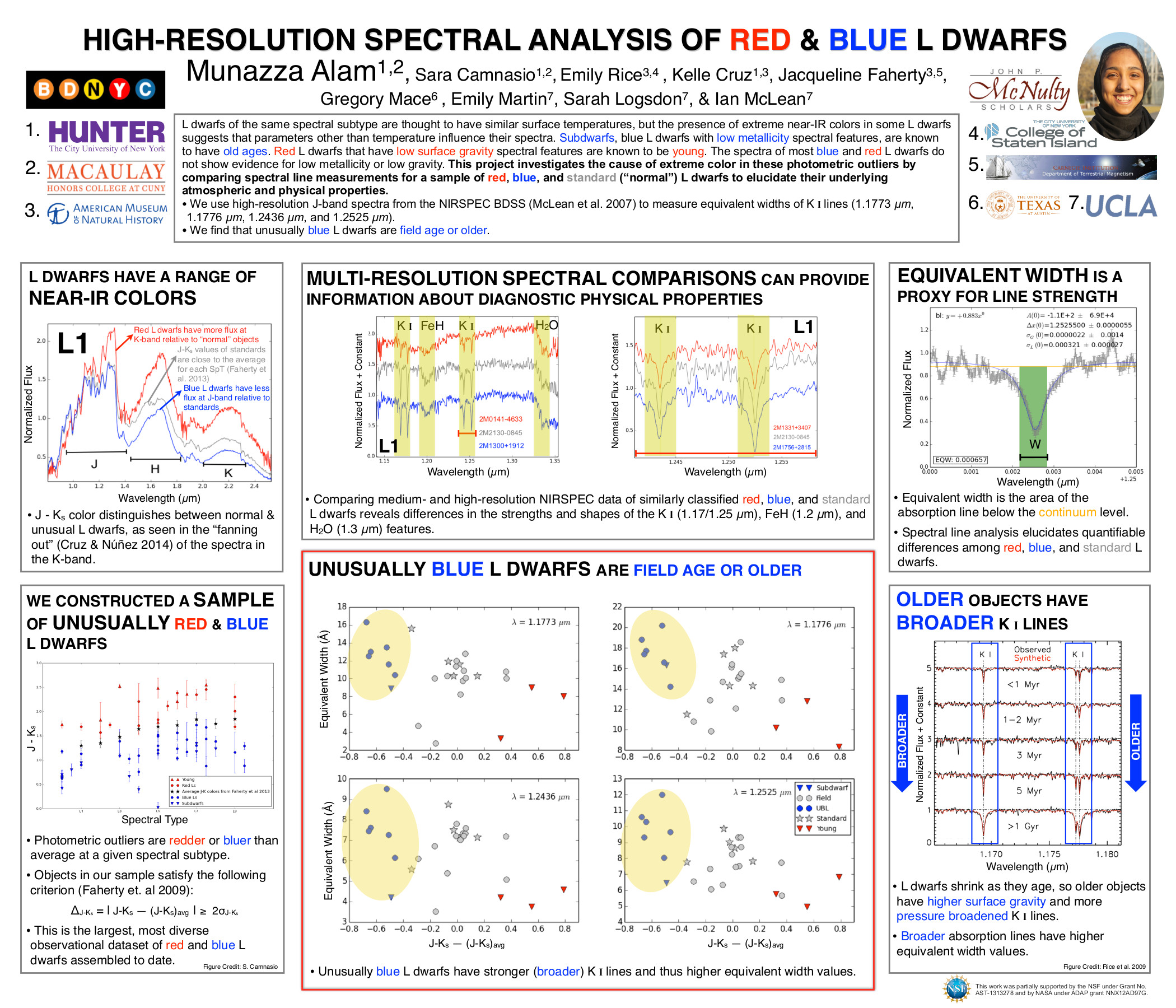
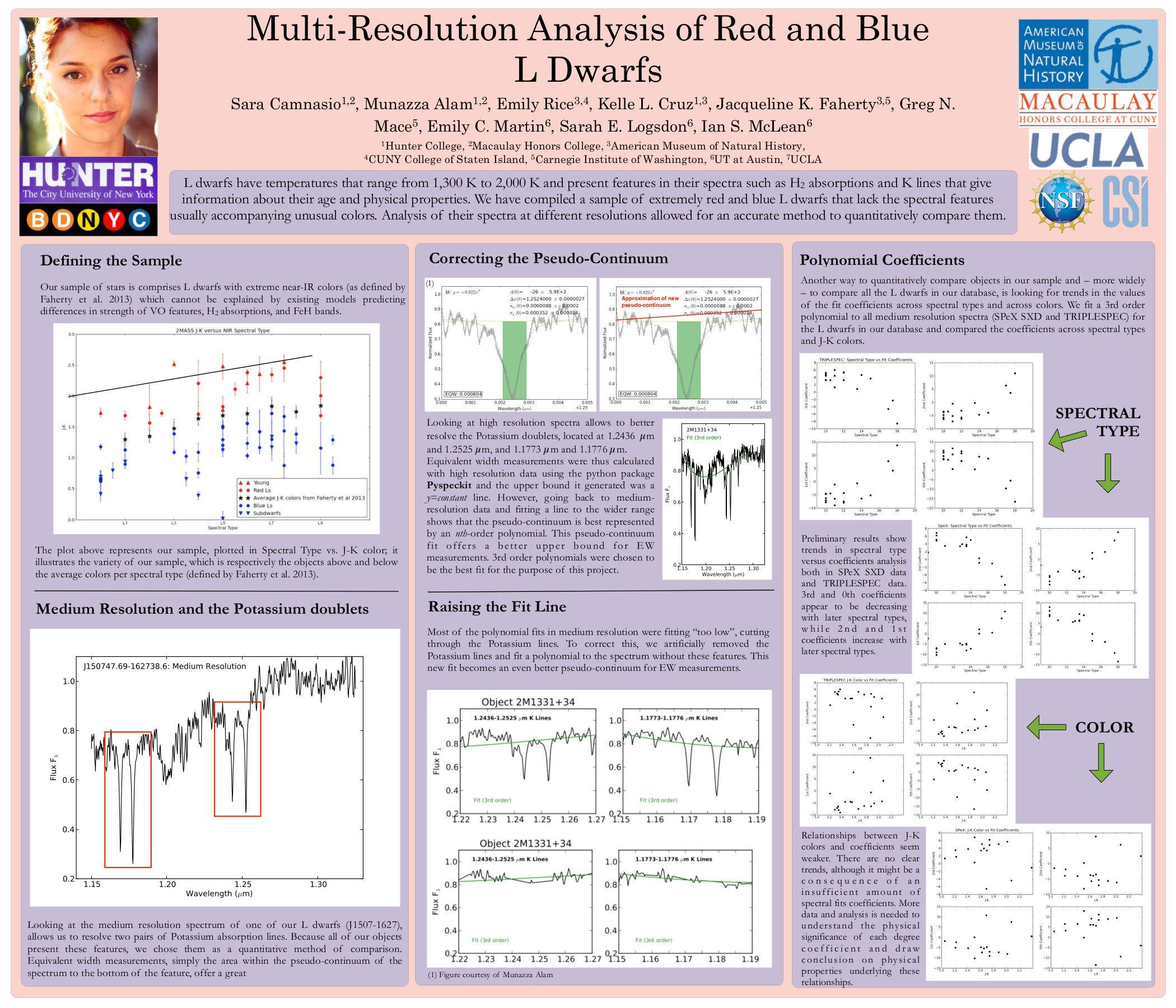
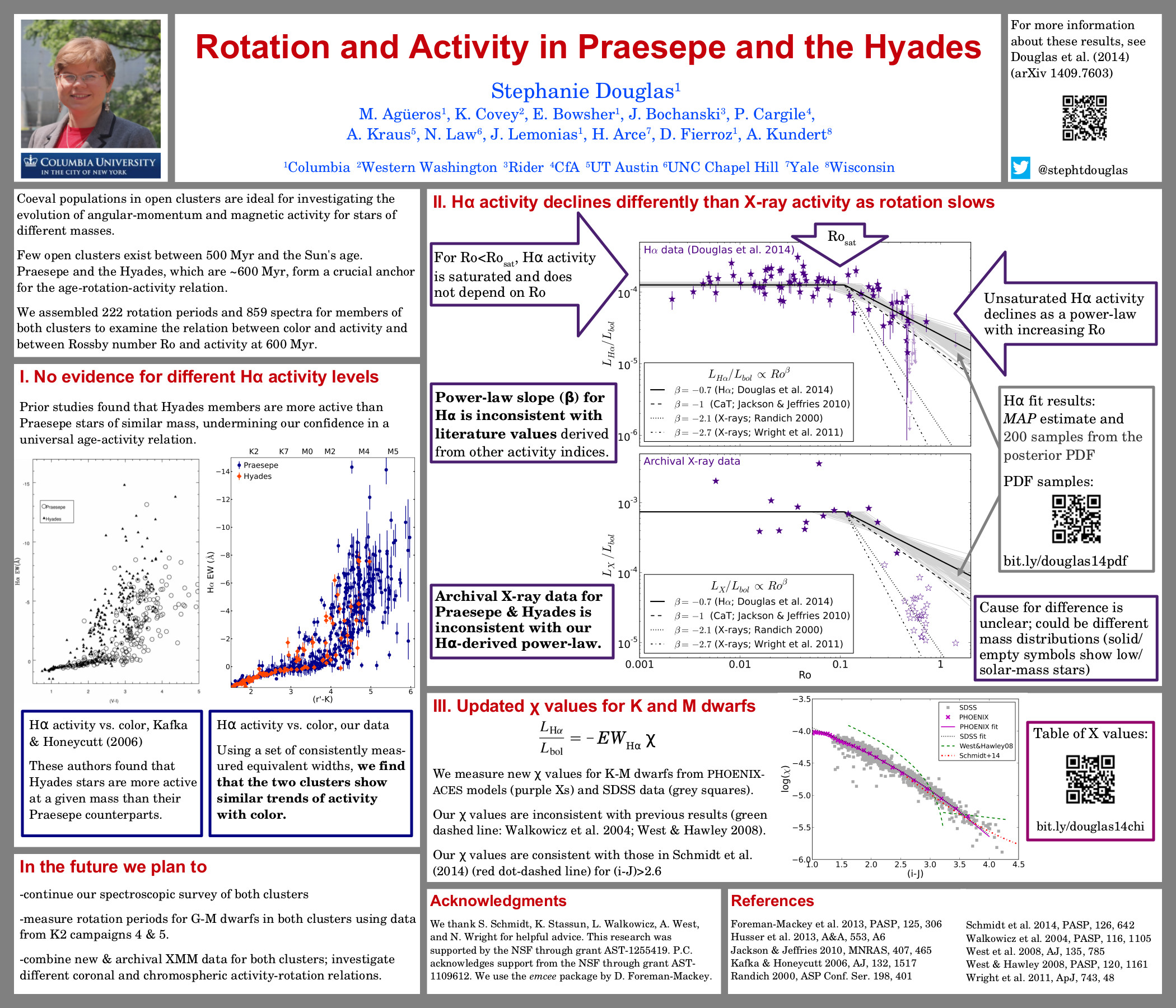
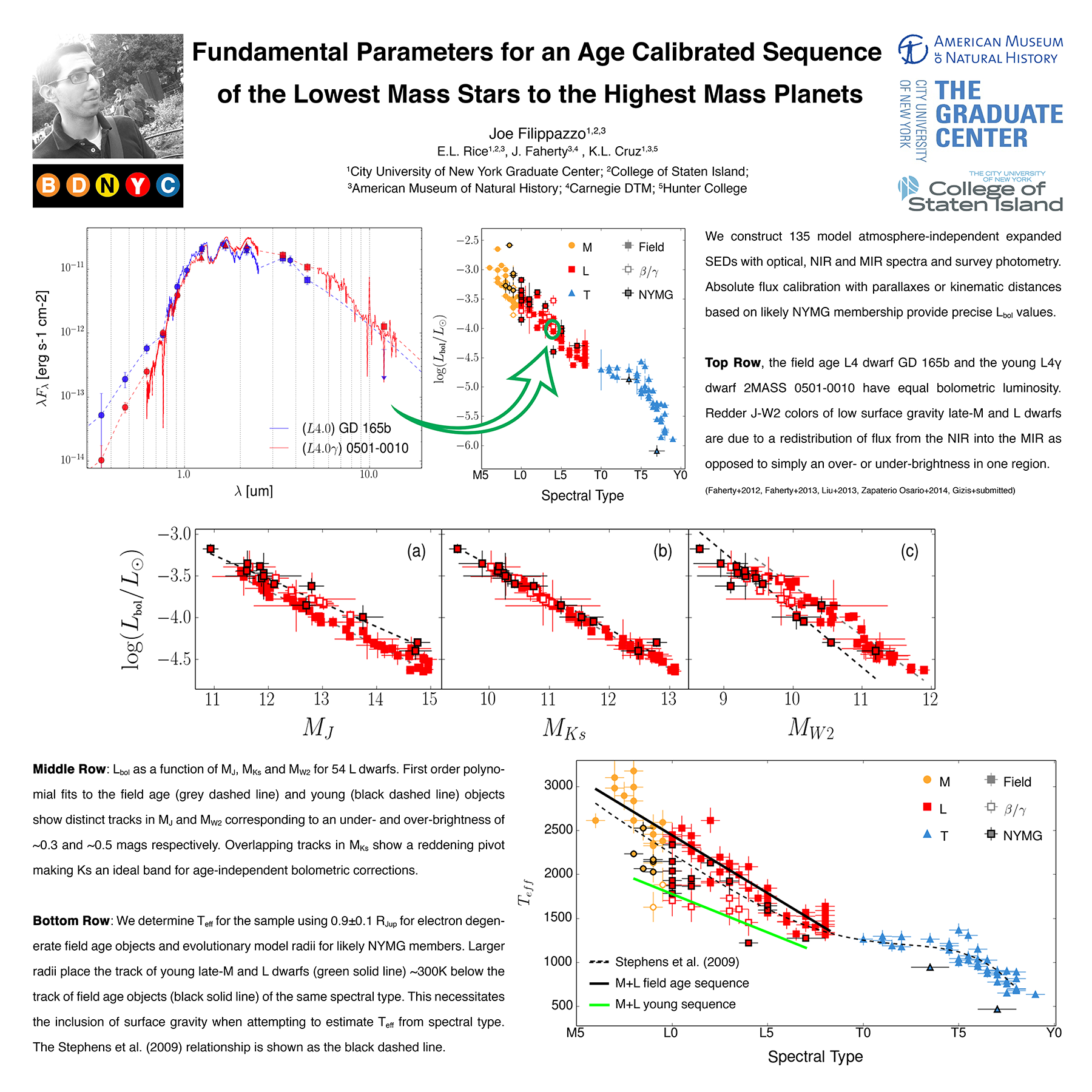
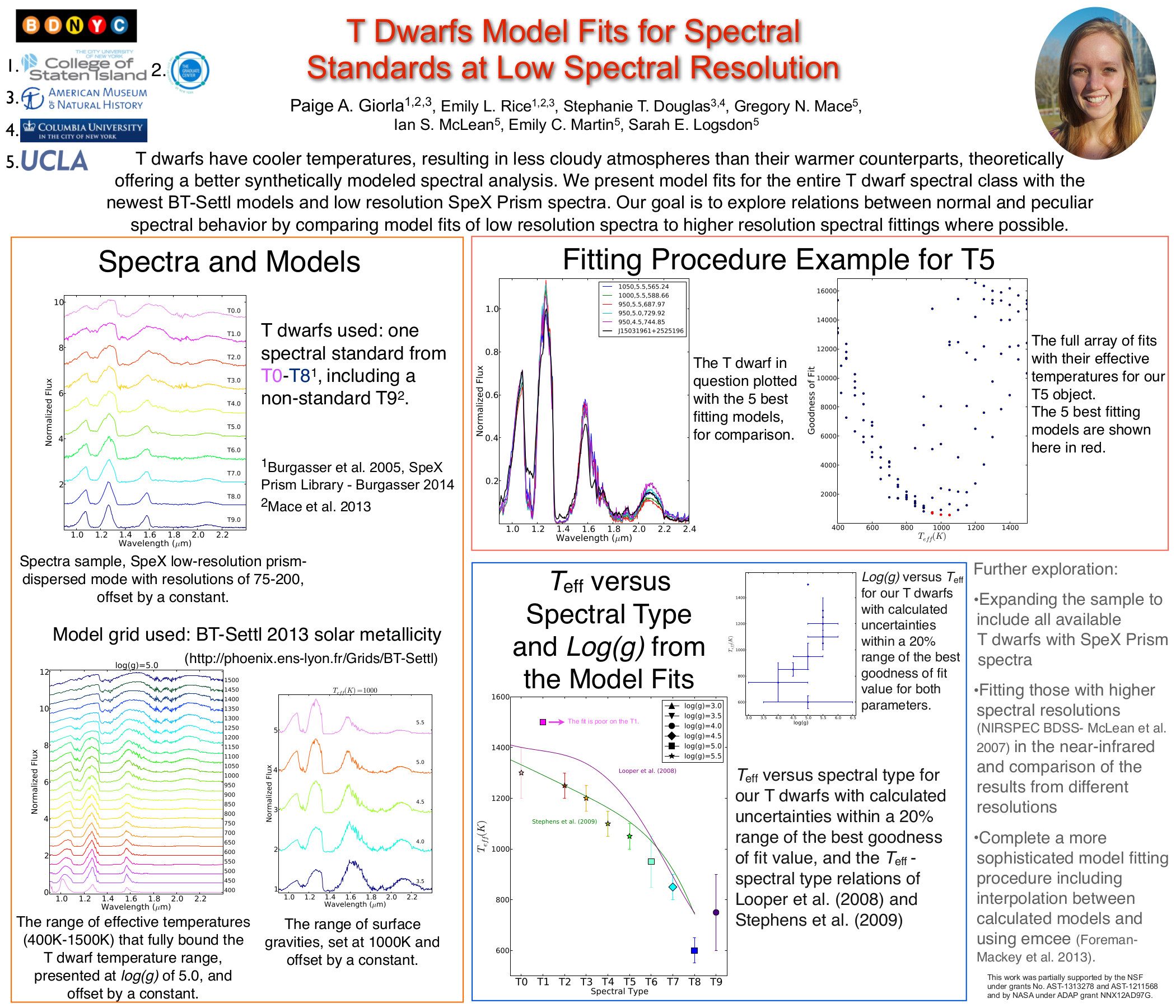
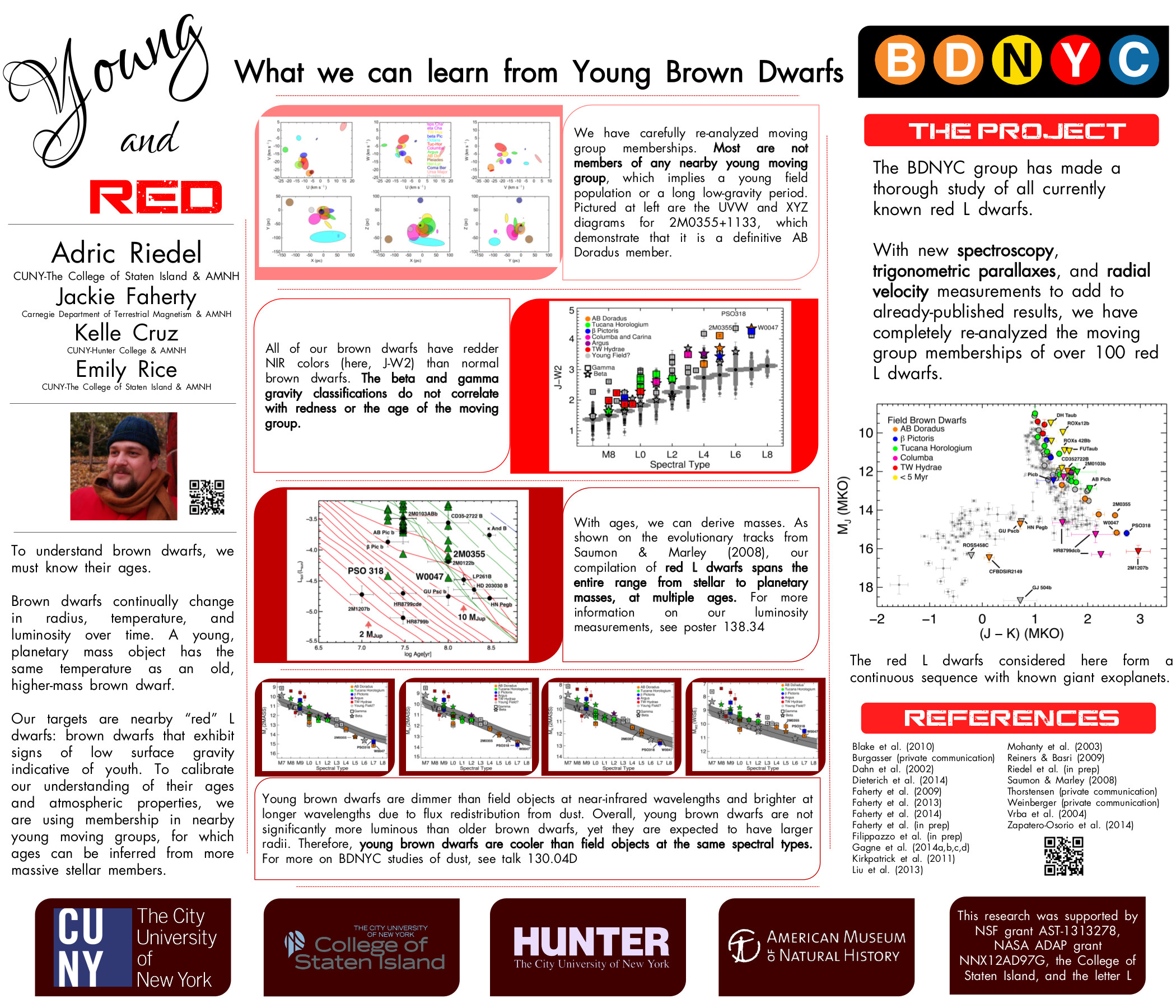
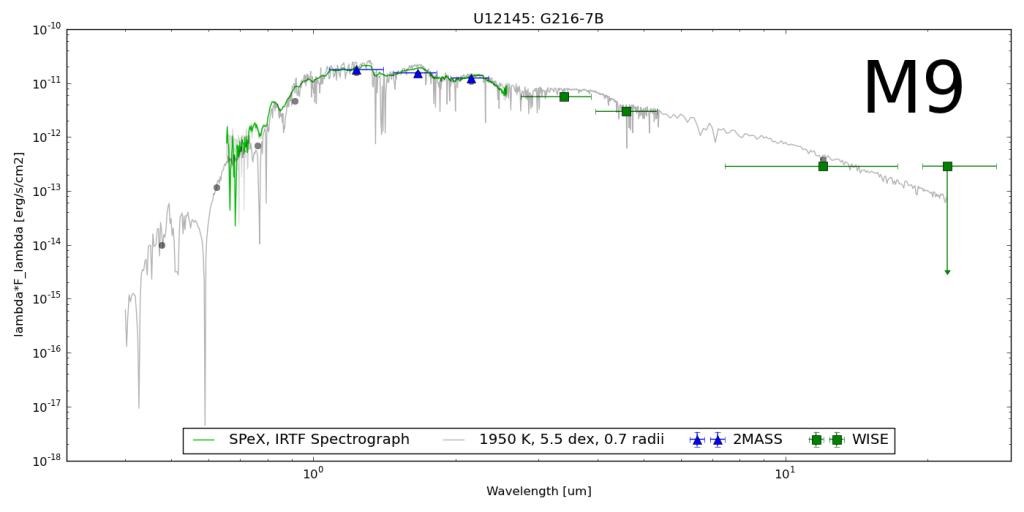
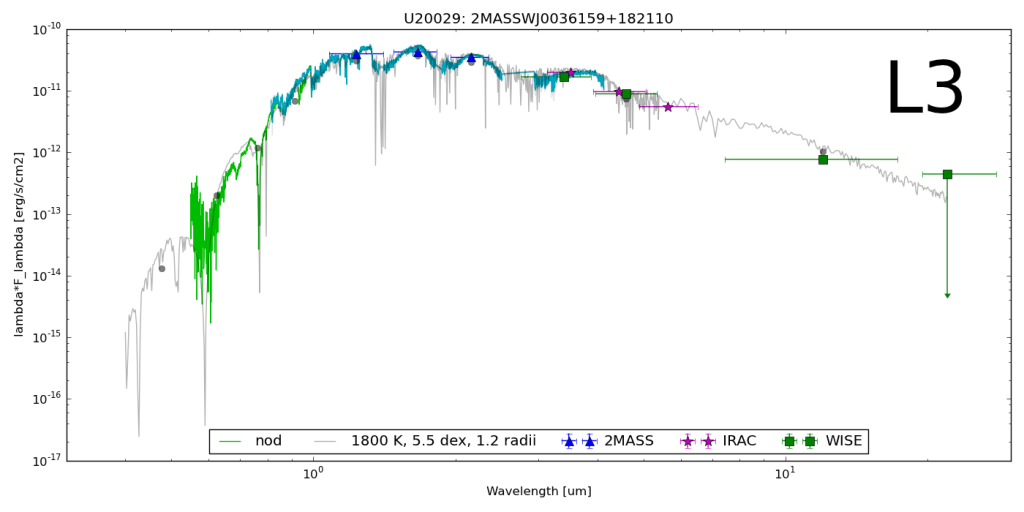
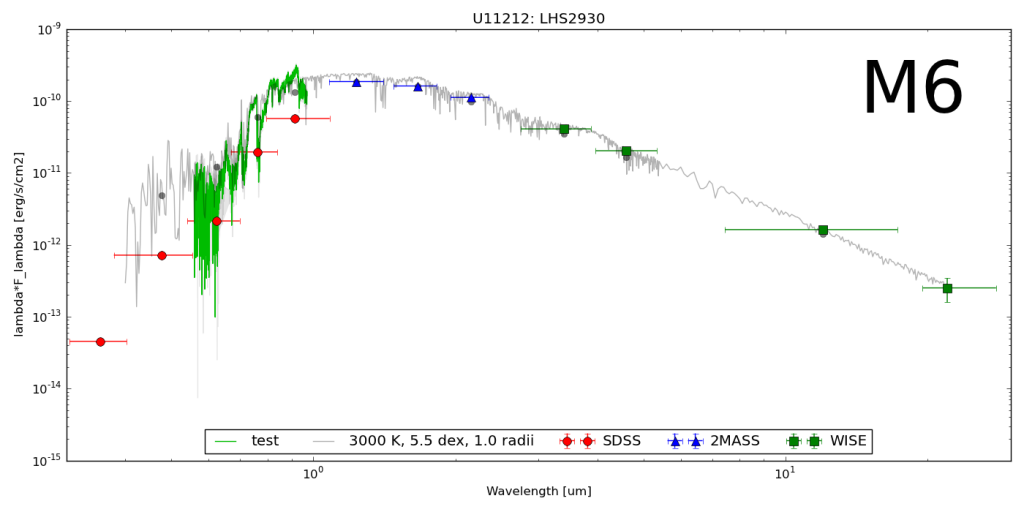
The goal here is to find a prescription of colors diagnostic of brown dwarf surface gravity. Since early optical as well as far infrared spectra and photometry are uncommon, the bands of interest should only include i and z from SDSS; J, H and Ks from 2MASS; and W1, W2 and W3 (but not W4 with only 10 percent detection) from WISE.
In order to find said prescriptions, I used the BT-Settl models (at solar metallicity ranging from 1000 – 3000 K in effective temperature and 3.0 – 5.5 dex in log surface gravity) to produce a suite of color-color and color-parameter plots.
One method I employed was to choose one effective temperature (in this case 2500K) and anchor the colors in one band that doesn’t vary much between high and low surface gravity, e.g. z-band. Then I chose the other two bands by one that was more luminous at low gravity and one that was more luminous at high gravity, e.g. W2- and J-band respectively.
Then the color-color plot of these bands looks like:
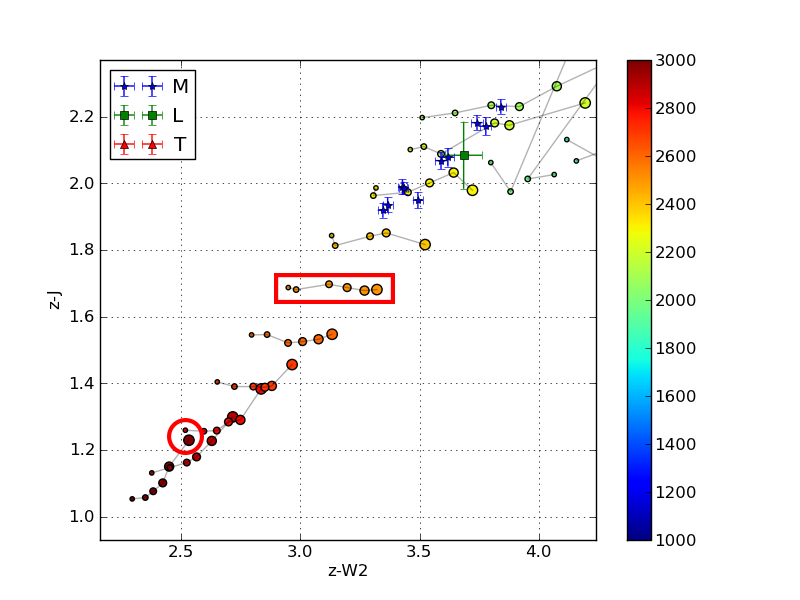
In this plot of z-J vs. z-W2 the smallest circles are objects with high surface gravity and the largest have low surface gravity (log(g) = 5.5 to 3.5 respectively). The light grey lines are iso-temperature contours.
In this particular case, there is little-to-no dispersion in z-J for Teff = 2500K (d = 0.009) and an appreciable dispersion in z-W2 for that same Teff (d = 0.32). Notice the tight vertical grouping (z-J) and dispersed horizontal grouping (z-W2) for the model objects of Teff = 2500K and varying log(g) in the red rectangle on the color-color plot above.
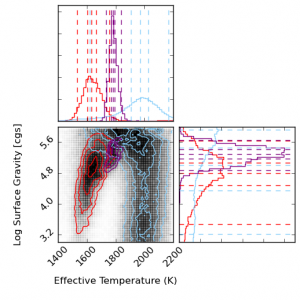
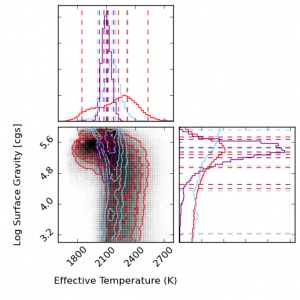
Double-checking with the color-Teff plots, we can see that the dispersion in z-J in the plot on the left is tiny and the horizontal offset in the color-color plot is due to the 0.32 magnitude dispersion in z-W2 on the right below.
Of course this is just a different way of looking at the same thing, but I might be able to find colors that are reliable indicators of gravity (and thus age) if I can find a bunch of these examples where the flux in the secondary and tertiary bands are flipped.
Of note is the fact that at this temperature in this color-color plot the points are also isolated, i.e. there are no degeneracies with objects of any other temperature. That means that if I find an object with a z-J = 1.65 or so, I know that it has an effective temperature of about 2500K. Then I can determine its age by seeing if its z-W2 color is closer to 3.3 (young) or 2.9 (old).
This of course does not work for all temperatures, as shown in the red circle in the color-color plot above. This demonstrates a degeneracy among hotter young objects (Teff = 3000K, log(g) = 3.5) and cooler old objects (Teff = 2800K, log(g) = 5.5) with a temperature difference of 200K.
Though there is no definitive combination of colors to identify the age of an object irrespective of temperature, what I have done here is found a collection of prescriptions that are reliable indicators of age over small temperature ranges.
The goal here was to investigate the atmospheric properties of known young objects and identify new brown dwarf candidates by producing extended spectral energy distributions (SEDs).
These SEDs are constructed by combining WISE mid-infrared photometry with our extensive database of optical and near-infrared spectra and parallaxes. The BDNYC Database has about 875 objects and the number of objects with parallaxes is about 250.
My code queries the database and the parallax measurements by right ascension and declination and then identifies the matches with enough spectra and photometry to produce an SED. Next, it checks the flux and wavelength units and makes the appropriate conversions to [ergs][s-1][cm-2][cm-1] and [um] respectively.
It then runs a fitting routine across BT-Settl models of every permutation of:
Once the best match is found, it plots the synthetic spectrum (grey) along with the photometric points converted to flux in each SDSS, 2MASS and WISE bands (grey dots). In this manner, the fitting routine guesses the effective temperature, surface gravity and radius simultaneously.
Here are some preliminary plots:
I figured the safest way to upload data to the database is to use an ascii file where you can enter the data as rows and columns, and then have the BDNYC code read the file and upload it for you. The method add_data does just that. This method is part of the BDNYC.py module, under the BDNYCData class.
Spectral average templates of 1–2.5 micron SpeX prism spectra of optically-classified field L dwarfs. Each of the three bands (JHK) are normalized across the whole band and plotted individually to remove the effect of the overall slope (color-term) of the spectrum. This allows the spectral features to be compared more directly.
The spectral features from L0 to L5 change gradually in the same direction, making a nice sequence in all three bands. The spectral features in the later type objects (L6–L8), however, do not follow the same trends as the earlier type objects and are therefore plotted separately.
The Planck functions for 2000, 1800, and 1600 K are shown (with arbitrary normalization) as dotted lines on the L0–L5 sequence. While molecular effects dominate the spectral morphology at most wavelengths, the shape of the J-band peak at 1.3 microns seems to be most sensitive to the underlying temperature-dependent Planck function rather than the strength of a particular absorption feature. It also looks like the slope of the H-band spectrum on either side of the water bands could also be modulated by the underlying Planck function rather than the water absorption itself.
This week I’ve started looking into making measurements of spectral features using Sherpa (program in Python). Before doing this, I wanted to understand what these measurements are, visually. These three measurements are Equivalent Width, Full Width Half Maximum (FWHM), and Line-to-Continuum Flux Ratio.
Shown in the figure above is the equivalent width (W) of an absorption line. The idea is you take the total area inside the absorption line, and create a rectangular box of the same area, extending from the continuum to the 0 flux line. The width of this box is the equivalent width. This measurement is used to describe the strength of the line (the higher the value, the stronger the line)!
Shown in the above plot is the Full Width Half Maximum (FWHM) of an emission line (it’s the same idea for absorption lines). You get the peak (maximum) value of the emission line, and draw a line at the half point. The width of the spectral feature at this flux value is the FWHM. For an absorption line, it’s the half of the minimum value instead of maximum. This measurement is used to describe how broadened the spectral feature is (the higher the value, the more broadened the line)!
Shown above is a sketch I made to illustrate the line-to-continuum flux ratio. In essence, you take the ratio of the flux of the continuum (the example used in the figure is a continuum flux of 1.0) to the flux of the max (or min) value of the feature (in the example, a value of 0.3) and subtracts it from 1. This measurement is used to characterize the depth of the line compared to the continuum (the higher the value, the deeper the line)! In the example above, the value is [1 – (0.3/1)] = 0.7
As illustrated above, these measurements describe a spectral feature. To recap, the equivalent width characterizes the overall strength of the line, the FWHM characterizes the width, or how broadened the line is, and the line-to-continuum flux ratio characterizes the depth of the line! Together, you can discern what the spectral feature may be saying about the physics of the scenario or target you are observing.
-Dan