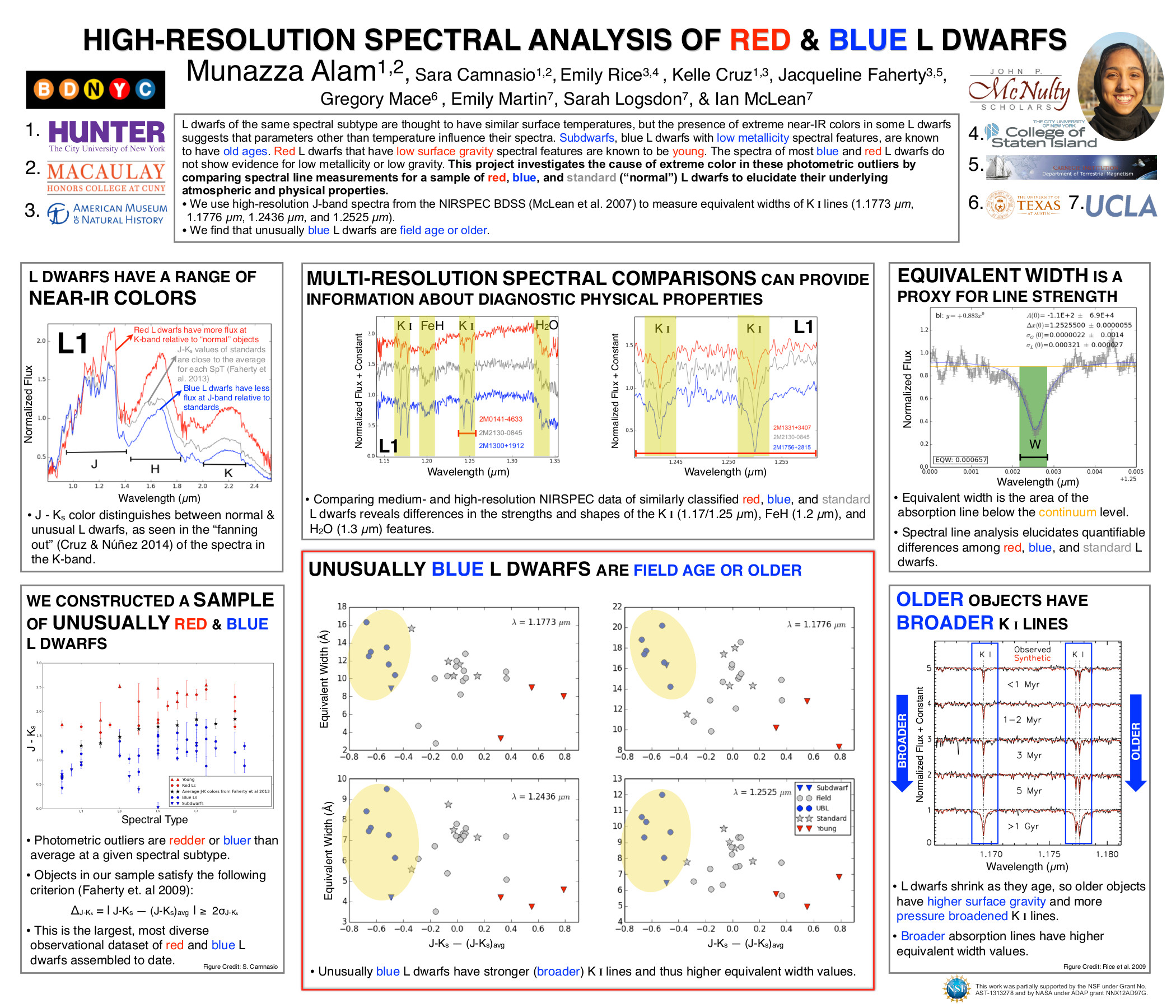
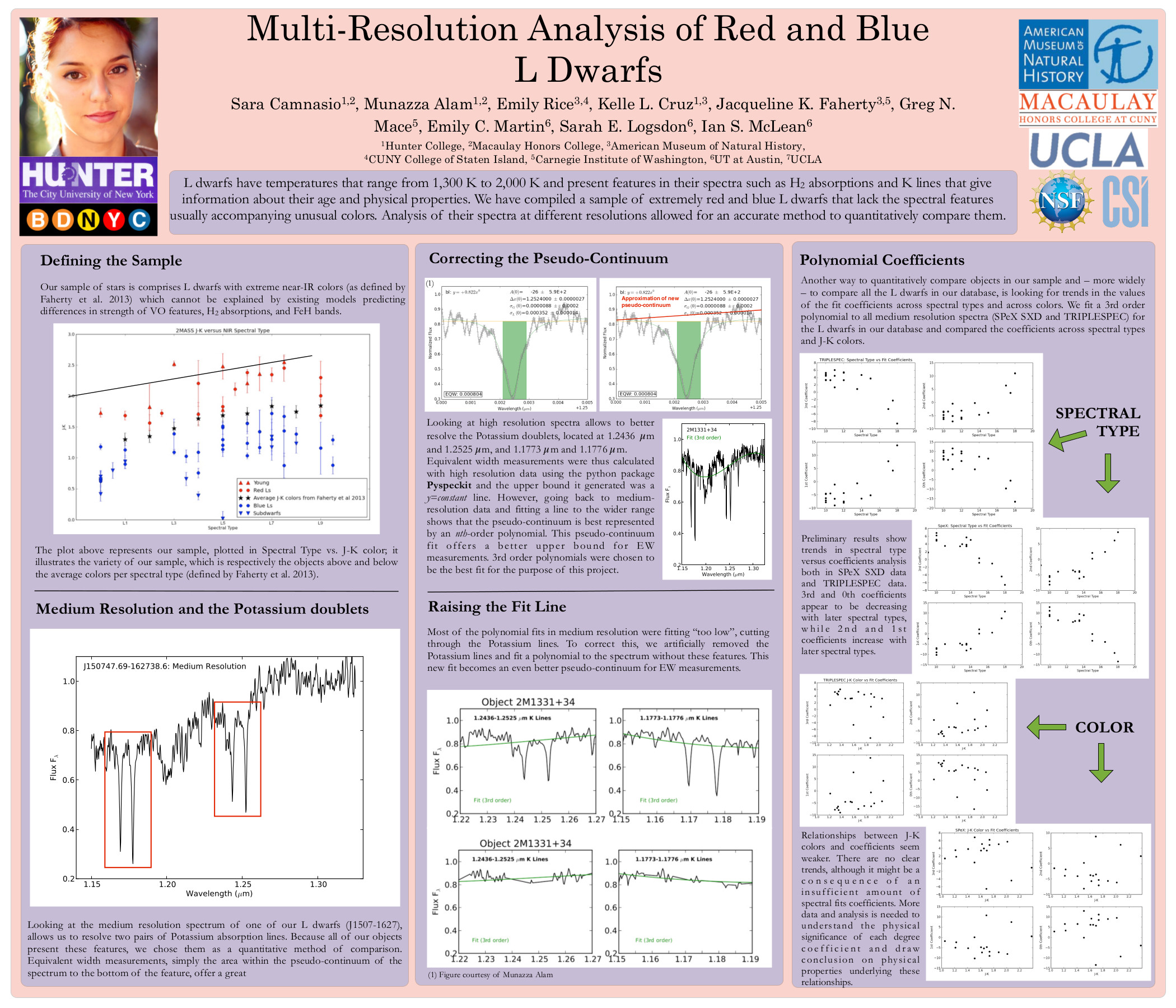
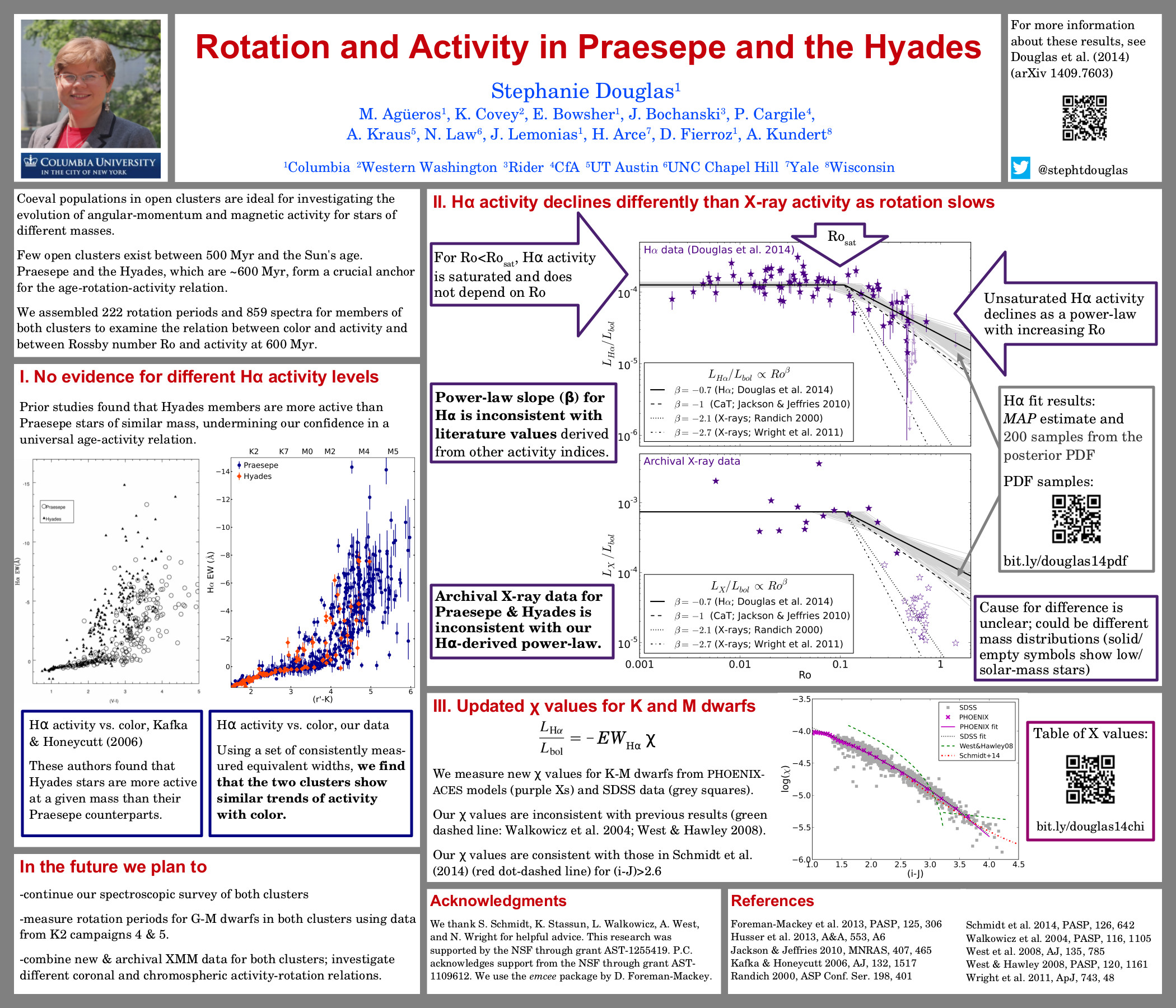
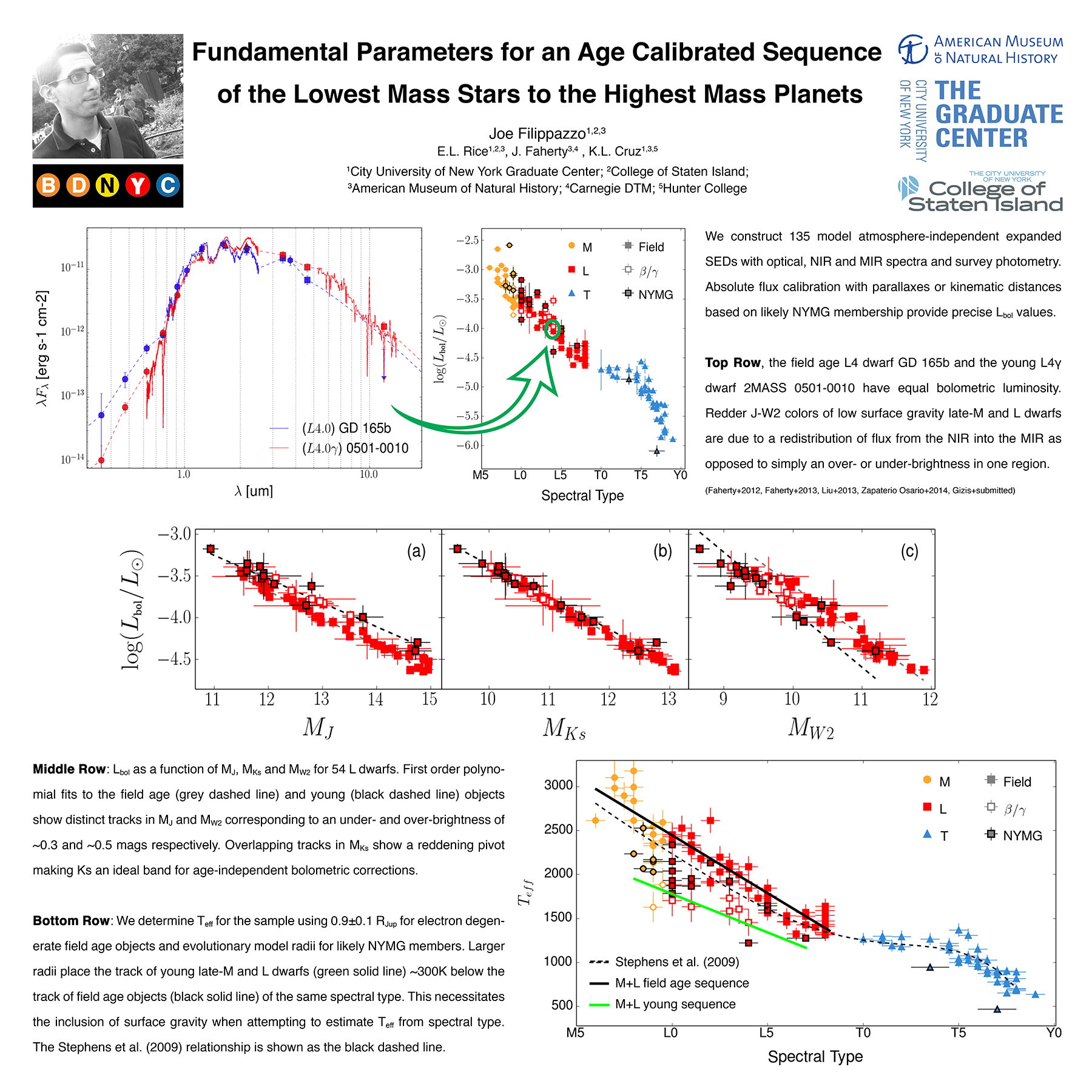
All observations have associated uncertainties which must be propagated through your analysis to a an uncertainty on a final result. The principle of uncertainty propagation is fairly simple:

$$!\sigma_x^2 = \sigma_u^2\left(\frac{\partial x}{\partial u}\right)^2 + \sigma_v^2\left(\frac{\partial x}{\partial v}\right)^2+\dots +2\sigma_{uv}^2\left(\frac{\partial x}{\partial u}\right)\left(\frac{\partial x}{\partial v}\right)+\dots$$

The first two terms on the right are the averages of the squares of the deviations in x produced by the uncertainties in observables u and v respectively. The third term on the right is the average of the cross terms, which cancel out if u and v are uncorrelated. Thus in most situations, a reasonable approximation is:

$$!\sigma_x^2 = \sum\limits_u\sigma_u^2\left(\frac{\partial x}{\partial u}\right)^2$$

Examples

A typical situation is the sum of two observables each with a multiplicative factor:

$$!x=au+bv$$

$$!\left(\frac{\partial x}{\partial u}\right)=a,\hspace{10pt}\left(\frac{\partial x}{\partial v}\right)=b$$

$$!\sigma_x = \sqrt{\sigma_u^2a^2 + \sigma_v^2b^2}$$

which is the oft used “summing in quadrature.”

Perhaps you have the product of two observables:

$$!x=auv+b$$

$$!\left(\frac{\partial x}{\partial u}\right)=av,\hspace{10pt}\left(\frac{\partial x}{\partial v}\right)=au$$

$$!\sigma_x = \sqrt{\sigma_u^2(av)^2 + \sigma_v^2(au)^2}=a\sqrt{\sigma_u^2v^2 + \sigma_v^2u^2}$$

Finally, perhaps you have the inverse of one observable times the exponential of another:

$$!x=\frac{a}{u}e^{bv}$$

$$!\left(\frac{\partial x}{\partial u}\right)=\left(-\frac{a}{u^2}\right)e^{bv},\hspace{10pt}\left(\frac{\partial x}{\partial v}\right)=\frac{a}{u}be^{bv}$$

$$!\sigma_x = \sqrt{\sigma_u^2\left(\frac{a}{u^2}e^{bv}\right)^2 + \sigma_v^2\left(\frac{a}{u}be^{bv}\right)^2}=\frac{a}{u}e^{bv}\sqrt{\frac{\sigma_u^2}{u^2}+\sigma_v^2b^2}$$

Easy!