The effective wavelength of a filter for narrow band photometry can easily be approximated by a constant and just looked up when needed. For broad band photometry, however, the width of the filter and the amount of flux in the band being measured actually come into play.
The effective wavelength of a filter is given by:
$$!\lambda_\text{eff}=\frac{\int \lambda \text{ }f_\lambda (\lambda)\text{ }S(\lambda)\text{ } d\lambda}{\int f_\lambda (\lambda)\text{ } S(\lambda)\text{ } d\lambda}$$
Where $$S(\lambda)$$ is the scalar filter throughput and $$f_\lambda$$ is the flux density in units of [erg s-1 cm-2 A-1] or [photons s-1 cm-2 A-1] depending upon whether you are using an energy measuring or a photon counting detector, respectively.
Here are the results for 67 brown dwarfs with complete spectrum coverage of the 2MASS J-band:
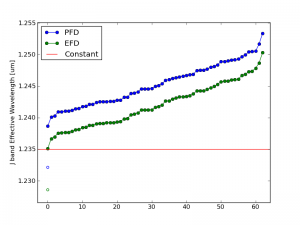
Effective wavelength values for the 2MASS J-band filter. Blue and green circles indicate lambda calculated using photon flux densities (PFD) and energy flux densities (EFD) respectively. Filled circles are for 67 confirmed brown dwarfs. Open circles are for Vega.
The red line on the plot shows the specified value given by 2MASS. For fainter objects like brown dwarfs (filled circles), the calculated effective wavelength of the J-band filter can shift redward by as much as 150 angstroms. Vega (open circles) shifts it blueward by about 30 angstroms.
The difference is small but measurable and demonstrates the dependence of the filter width, source spectrum, and detector type on the effective wavelength $$\lambda_\text{eff}$$ while doing broad band photometry.
