Author Archives: Kay

Fitting a power law to data

Posted on by
1

I wanted to fit a power law function to data, not a polynomial. Here’s how I did it.

I used the least squares method.

How to fit a power law to the data

power fit to L4 data

Example of a power law fit to data

If you prefer other types of functions, just change the function form to whatever you want to fit when you define it.

The inputs for leastsq are the error function (difference between data and a function you want to fit) and initial conditions. When full_output = nonzero, it returns the covariance matrix in addition to the parameters that minimize the sum of squares of the error function.

What would you fit a power law function to?

Formatting Plots for Paper in Python

Posted on by

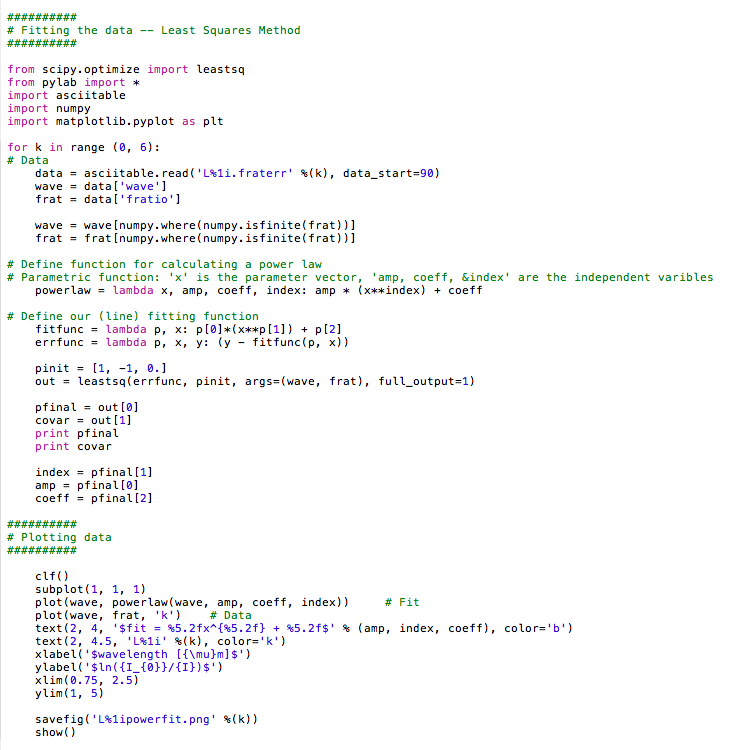
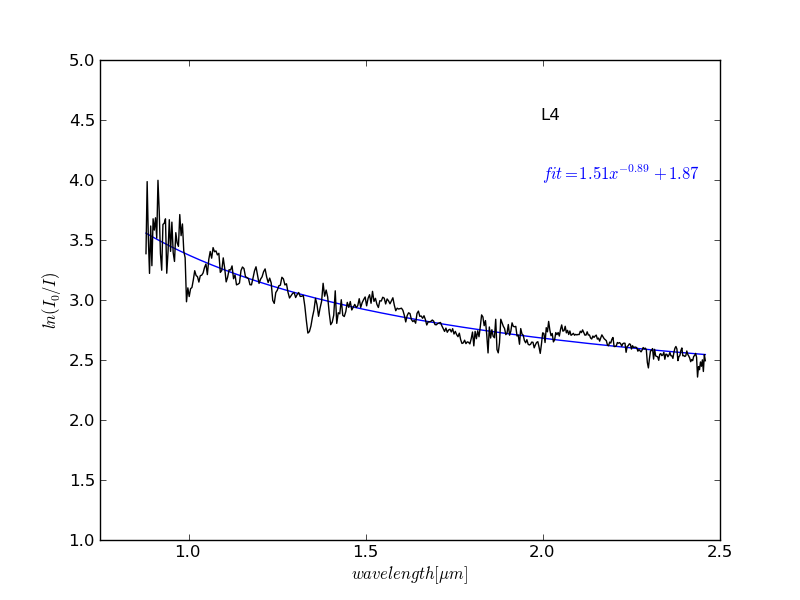
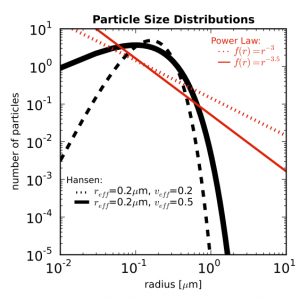
Say you have a nice figure and you want to make it look good in your paper. Figures in  papers will be in the dimension of 8.9cm x 8.9cm (3.6in x 3.6in) so you want to make them clearly legible when shrunk to this size. Something like this.


You can set the size of your figure by doing

figure = matplotlib.pyplot.figure(figsize=(3.6, 3.6))

then you can check what it looks like in that dimension on your screen.

You may need to set the size of the plot so that all the axis titles are inside the figure. These parameters worked for me.

subplot = figure.add_subplot(1, 1, 1, position = [0.2, 0.15, 0.75, 0.75])

In the position bracket are [left (y axis position, x_0), bottom (x axis position, y_0), width (length of x axis), height (length of y axis)] of your plot.

To set the x and y limits on the axes, use set_xlim([xmin, xmax]) and set_ylim([ymin, ymax]).

To make the plot simple, you want to keep the variation of color and style to a minimum. Maybe combinations of a couple of colors and a couple of simple line styles. You can edit line width, line color, and line style by adding arguments to your plot command. 
Continue reading →