Molecules can store energy in 4 different ways: translation (whole molecule moves in each of 3 Cartesian coordinates), rotation (whole molecule rotates—linear molecules can rotate around 2 axes, nonlinear around all 3 axes), vibration (bonds stretch and contract—3N-5 kinds of vibrations for linear molecules, 3N-6 for nonlinear), and electronic (ground state vs. excited). The energy absorbed in electronic transitions is usually in the UV-visible range, that for vibrations is in the IR range, for rotations in the microwave range, and the transition energy for translations is basically infinitesimal. This is because electronic transitions require the most energy, then vibrations, rotations and finally translations require the least. With high enough resolution, rotational transitions can be seen in vibrational spectra, with the rotational transitions giving structure to the vibrational absorption peaks.

Figure 1: An energy diagram showing the relative energies for rotational, vibrational, and electronic transitions and how they overlap.3
The energy of rotational and vibrational levels can be calculated separately and summed. Vibrations can be modeled using the simple harmonic oscillator—the potential energy of which comes from Hooke’s law. Rotational energy of a molecule can be calculated by assuming the molecule acts as a rigid rotor and solving the corresponding Schrodinger Equation. Both of these types of energy are quantized, which accounts for the vibrational (v) and rotational (J) quantum levels in the equation.
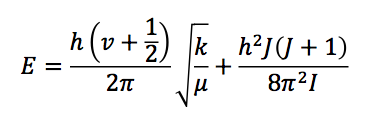
This equation will give energy levels in Joules. Vibrational spectroscopists generally use units of wavenumbers, or cm-1, though, which can be found by dividing the entire equation by hc.
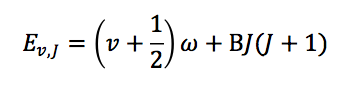
where
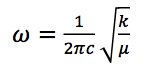 and
and
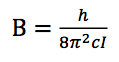
- v: vibration quantum number (0,1,2,…)
- J: rotation quantum number (0,1,2,…)
- k: spring constant/strength of bond
- μ: reduced mass
- I: moment of inertia, where is bond length
- B: rotational constant
I began looking into this to explain why multiple carbon monoxide absorption peaks appeared where they did in my near-IR spectra at 2.29 and 2.32 microns or 4367 and 4310 cm-1. I was able to calculate the correct 2.29 μm peak by subtracting the energy where v=0 and J=8 from the energy where v=2 and J=10. This means that these peaks are due to the first vibrational overtone of CO, i.e. Δv=2 instead of 1. The peak at 2.32 and any other peaks around the same area can be found by going from different rotational energy states, 6 to 8, 4 to 6, etc. ΔJ for CO is usually ±2 because it is a linear molecule.
- McQuarrie, Donald A. Quantum Chemistry. 2nd ed. Sausalito: University Science Books, 2008.
- Atkins, P.; de Paula, J. Physical Chemistry. 8th ed. New York: W. H. Freeman and Company, 2006.
- “Electronic Spectra of Organic Molecules”. Organic Chemistry. http://www.organicchemistry.com/electronic-spectra-in-raman-spectroscopy/. Accessed July 24, 2014.
On solving the Rigid Rotor Schrodinger Equation:
http://chemwiki.ucdavis.edu/Physical_Chemistry/Quantum_Mechanics/Quantum_States_of_Atoms_and_Molecules/7._Rotational_States/Solving_the_Rigid_Rotor_Schrödinger_Equation
Special thanks to Professor Andrew Crowther.
