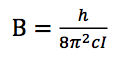Let’s say you have a set of data in an Excel document or Google spreadsheet* and you want to share it with the public by posting it on your webpage. You no longer have to create a static HTML table; in fact, Google allows for embedding a table on a webpage that is updated as the original Google Doc is updated. The way to do it is by creating what is called a “live” spreadsheet.
The process is very simple and the results will definitely save you a lot of time.
- First, import your Excel file in Google Docs or open your Google spreadsheet;
- File > Publish to the Web…;
- Check the box that says “Automatically republish when changes are made”;
- Click “Start Publishing”;
- Change “Get a link to the published data” from “Web page” to “HTML to embed in a page”;
- Copy and paste the HTML code generated (should start in “<iframe”) in an HTML-enabled space on your webpage.
At this point, you would just need to make changes on your Google spreadsheet to see the table on your website edited as well. In my testing, the automatic update always worked flawlessly; however, if that does not happen:
- Open your Google Doc;
- File > Publish to the Web… > Republish now.
- Magic! You should see the table data updated on your website.
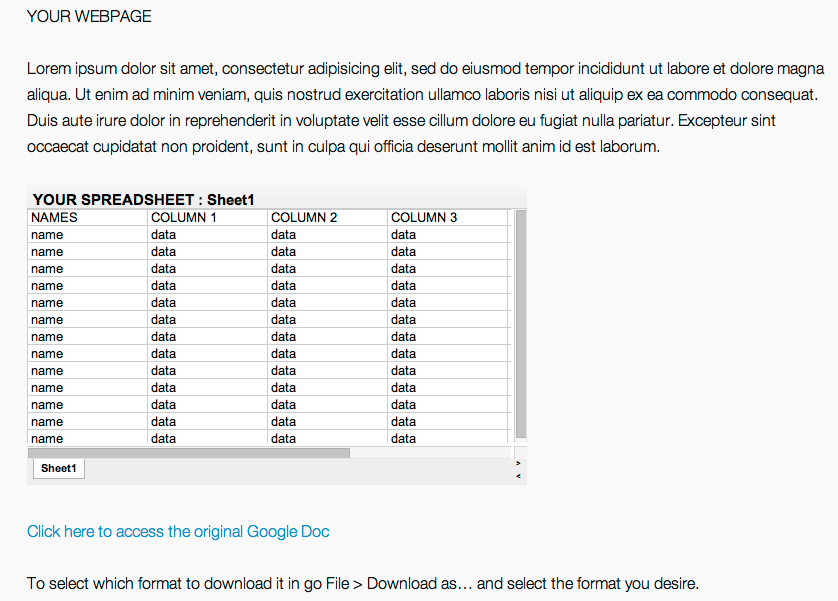
This is how the embedded spreadsheet will appear on your webpage.
You can now adjust width, height and frameborder by changing the values in the <iframe> code in HTML mode.
Linking to the original Google Doc
Now, what if you also want users to be able to access your original table?
The way to do this is also very easy and I found it here (theBioBucket).
In your webpage, in HTML mode, write a code using the standard HTML notation to create a link <a href=”URL”> YOUR TEXT HERE </a>
The URL you will have to plug in is your Google doc one, found under “Share…”:
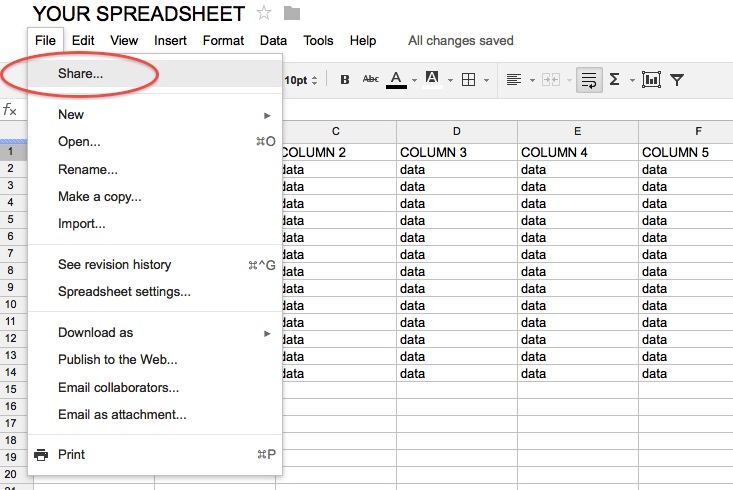
Click “Share…” under “File”

Grab the URL circled and paste it in the HTML code.
Once you’ve done that, you can simply write something like “Click here to access the Google document for this table” in the YOUR TEXT HERE space, and… all done!
A Google account is not necessary to view the original Google Doc. Any user on the web can access the original Google spreadsheet in view-only mode. They won’t be allowed to alter the original table in any way, but they will have access to a spreadsheet downloadable in different formats (e.g. .pdf, .csv, .txt). To download, simply click File > Download as… and save the document on your computer in all the formats available in Google Docs.
* Note: This method works with every format available in Google Docs but this post focuses on spreadsheets.



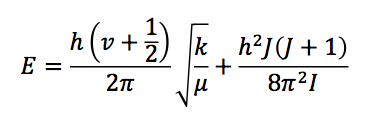
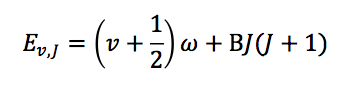
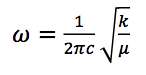 and
and